고등학교 [기하]를 배운 학생이라면 좌표평면 내에서 2차원 벡터를 다뤄봤을 것이고, 더 나아가 좌표공간에서의 3차원 벡터를 다뤄봤을 것이다. 이때까지 고등학교에서 배운 벡터는 직관적으로 다음과 같이 생각할 수 있다.

크기와 방향을 가진다는 것이 그간 실수 정도만 가지고 놀던 고등학생에게는 매우 생소한 직관이다.
벡터 미적분학에서는 이름에 걸맞게 벡터를 다룬다. 보통 머릿속에 떠올리기 좋기 때문에 2~3차원까지만 다루기는 하지만 4차원 이상의 벡터를 다룰 때가 있다.
고등학교 때 배우는 벡터의 기본 연산(덧셈, 뺄셈, 스칼라 곱셈, 내적)은 생략한다. 다차원 벡터에서도 2, 3차원 벡터와 같은 방식으로 연산을 적용하면 된다.
벡터는 다음과 같이 표현할 수 있다.

오마이갓!! 도대체 수식에 있는 기호는 다 무엇인가.
∈기호는 고1때 학원 선생님으로부터 별로 중요하지 않아서 대충해도 된다는 말을 들은 학생이라면 까먹었을테다. 그러면 다시 [집합과 명제]를 공부하고 오길 바란다. 앞으로 저런 기호가 수도 없이 나올 것이다.
N과 R은 처음봤을텐데 각각 자연수 집합과 실수 집합이다. (정수는 저 글씨체 그대로 Z로 나타낸다.)
R^n이라 하는 것은 차원을 나타내는데 1차원은 R, 2차원은 R^2, 3차원은 R^3 이런식이다. 이는 곱셈 기호를 이용해서 표현할 수도 있다.
위 수식에서 x벡터는 각각의 원소가 실수인 다차원 벡터이다.
혹시나 맹목적으로 벡터하면 화살표를 떠올린 학생이라면 이참에 그 연결성을 조금 지우길 바란다.
2차원과 3차원 벡터는 화살표로도 충분히 생각할 수 있지만 4차원 5차원 벡터는 어떻게 떠올릴 것인가? 이 경우 벡터를 화살표가 아닌, 수 여러 개를 모은 것이라고 봐야할 것이다.
앞으로 나올 2, 3차원 벡터들도 뭔가 의미가 있는 화살표들이라기 보다는 수의 다발로 보는 것이 도움이 될 때가 많다.
[기저 벡터]
[기하]를 배웠다면 임의의 벡터를 (1, 0)과 (0, 1)의 합으로 나타내는 문제들을 풀었을 수도 있다. 여기서 나온 (1, 0)과 (0, 1)이 2차원의 기저 벡터이다. 즉, 좌표축 방향의 단위 크기를 나타내는 벡터들이다.
어떤 선형 변환(이후에 살펴볼 것이다)에 대해서 크기가 1이 아닐 수도 있기 때문에 단위 크기라고 써놓았다.
3차원 공간에서는 (1, 0, 0), (0, 1, 0), (0, 0, 1)이 기저 벡터일 것이다.
기호 머리 위에 ^(hat)을 얹어서 기저를 표현할 수 있고 x^, y^, z^ 또는 i^, j^, k^ 등으로 표현한다.
사람에 따라서 i, j, k 위의 기호를 ^이 아닌 일반 화살표로 나타내는 경우도 있고 벡터 e_i 로 표현하는 경우도 있다.
(필자는 i^, j^, k^ 방식을 매우 선호한다.)
위에서 나타낸 다차원 벡터는 결국 기저 벡터의 선형 결합으로 나타낼 수 있을 것이다.
+ 선형 결합
어떤 요소들의 스칼라 곱을 더한 것을 선형 결합이라고 한다.
벡터 x = x_1 * e_1 + x_2 * e_2 + ... + x_n * e_n
수식을 보면 bold 체로 되어있는 곳과 아닌 부분이 있는데 bold로 된 부분이 벡터이다.
보통 이런식으로 벡터를 표현하기도 한다. (필자는 고등학교 때 물리 관련 자료를 살펴보다가 저 notation 때문에 고생한 적이 있다.)
[내적]
내적은 (a, b)·(c, d) = ac + bd로 정의가 된다.
벡터의 내적으로부터 우리는 다음과 같은 사실을 유도할 수 있다. (삼각함수 합차공식)
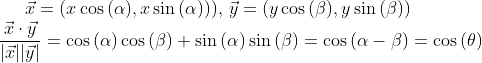
따라서 내적의 정의에서 고등학교에서 공부한 (a, b)·(c, d) = |(a, b)| |(c, d)| cos θ 가 유도된다.
내적으로 벡터의 크기를 정의할 수 있다.

이 정의는 우리가 직관적으로 생각할 수 있는 벡터의 크기로도 적합하다.
좌표평면에서 두 점 사이의 거리를 피타고라스의 정리로 구하는 방법은 두 말 할 것 없다.
어떤 직육면체의 공간 대각선을 구하는 방법을 생각하면

세 변의 제곱의 합의 제곱근으로 계산되는 것이 위에서 본 벡터의 크기에 대한 정의와 일치한다는 것을 알 수 있다.
- Theorem 1: Cauchy-Schwarz inequality
코시-슈바르츠 부등식은 현재는 교육과정에서 빠진 것으로 기억하며 이전 교육과정에서는 다음과 같이 설명했다.
(ax+by)^2 <= (a^2+b^2)(x^2+y^2)
그리고 벡터로는 다음과 같이 설명한다. 모든 벡터 x, y에 대해 (단, 등호는 x와 y가 비례할 때 성립한다.)

x, y를 각각 (a, b), (x, y)로 두면 고등학교에서 설명하는 부등식이 성립함을 알 수 있다.
증명>>

- Theorem 2: Triangle inequality

삼각형의 두 변의 길이의 합은 나머지 한 변의 길이보다 크다는 것은 누구나 아는 사실이다.
때문에 다음 수식은 성립한다.

증명>>
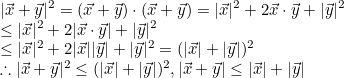
[행렬]
벡터처럼 행렬도 수를 모아놓은 구조인데 벡터보다 더 많은 줄을 갖고 있다는 것이 차이점이다.
행렬을 표현할 때는 보통 대문자 알파벳을 주로 사용한다.
mxn 행렬은 다음과 같이 표현한다.

사람들이 많이 헷갈려 하는 부분인데 행이 가로줄이고 열이 세로줄이다.
mxn 행렬이라면 행이 m개, 열이 n개임을 알 수 있다.
행렬의 각 원소는 위 식처럼 표현을 하는데, 행렬의 이름처럼 첫 숫자가 행 번호, 두 번째 숫자가 열 번호를 나타낸다.
(행과 열의 번호가 두 글자 이상이라면 A_112가 11행 2열인지 1행 12열인지 헷갈릴 것인데, 우리가 다룰 행렬은 이 정도 크기까지는 다루지 않으며 혹시나 다루더라도 A_1 12 또는 A_1,12 처럼 표현하면 될 것이다.)
필자는 앞으로 행렬을 표현할 때, mat(m, n)이라는 기호를 써서 나타내려고 한다.
[전치 행렬]
행렬의 행과 열을 뒤집어주는 것을 전치 연산이라고 한다.
중요한 부분은 선형대수학에서 배울 것이므로 여기서는 벡터와 행렬이 어떻게 동일시 되는지만 확인하고 넘어갈 것이다.

위와 같이 열로만 이루어진 행렬을 열벡터라고 하며 벡터와 동일시될 수 있다.
전치 행렬의 기로는 맨 밑의 줄처럼 윗 첨자 T를 써서 나타낸다.
다시 돌아와서, 위에서 본 A 행렬은 다음과 같이 나타낼 수 있다.

[행렬의 연산]
덧셈, 스칼라곱과 같은 경우는 우리가 벡터에서 하던 것처럼 각 원소에 대한 연산을 진행해주면 된다.
하지만, 행렬끼리의 곱은 조금 더 복잡한 연산 과정을 필요로 한다.
mxn 행렬 A, nxp 행렬 B에 대해서 다음이 성립한다.

계산을 하면 할수록 아마 익숙해질 것이다.ㅋㅋ
기억하기 쉬운 그림을 제공하겠다.
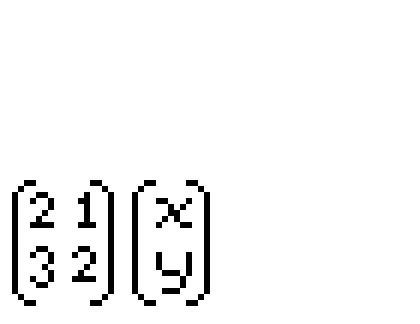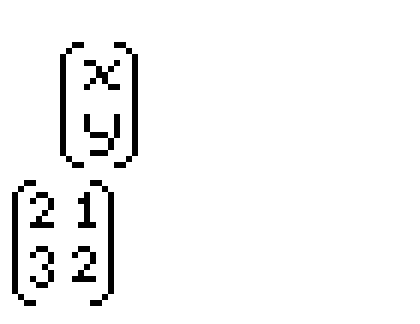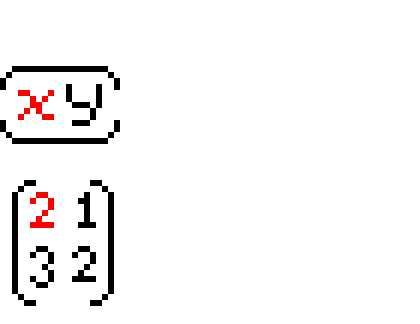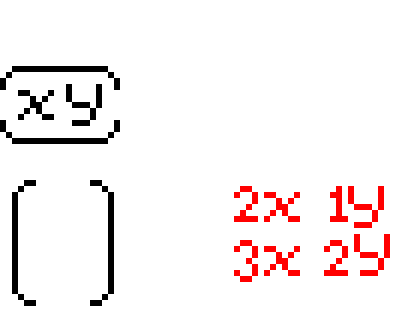
행렬끼리의 곱셈에서 중요한 점은 교환법칙이 성립하지 않는다는 점이다.
AxB는 A의 열의 수와 B의 행의 수가 같아서 연산이 가능하지만, BxA는 그렇지 않다.
만약 두 행렬 다 행과 열이 같은 정사각 행렬이라고 했을 때, AxB와 BxA를 계산하면 그 값이 다르다는 것을 알 수 있다. (직접 계산해보아라.)
B가 열벡터일 때 AxB는 또 다른 열벡터 하나를 결과로 내놓는다.
이 경우에서 A를 선형 변환(Linear Transformation or Linear Deformation)이라고 하며

로 표현할 수 있다. 물론 행렬끼리의 곱에서도 선형변환이라고 한다.
밑의 식은 map 표현으로 정의역과 치역의 직접적인 관계를 나타낼 때 주로 쓴다.
[행렬식] : Determinants
2x2 행렬식부터 정의한다.
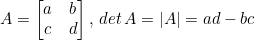

4x4 이상의 경우에는 3x3 행렬의 행렬식을 계산한 것처럼 +, -부호가 반복되는 항을 가지고 있다.
- 행렬식이 어떤 의미를 가지고 있는가?
기하학적으로는 두 열벡터로 이루어진 평행사변형의 넓이라고 할 수 있다.
다음과 같이 주어진 평행사변형에 대해
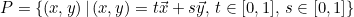

평행사변형의 넓이가 det A의 절댓값으로 나온다는 것을 알 수 있다.
같은 방법으로 3차원 행렬식은 평행육면체의 부피와 같음을 유도할 수 있다.
+ 선형변환과 행렬식을 다시 한 번 살펴보자.
어떤 변환 A가 있을 때, 행렬식은 (1, 0)과 (0, 1)의 변환된 벡터로 이루어진 평행사변형의 넓이라고 볼 수 있다.
https://angeloyeo.github.io/2019/07/15/Matrix_as_Linear_Transformation.html
행렬과 선형변환 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
위 사이트에서 선형 변환으로 기저를 변화시킴과 동시에 기저로 이루어진 평행사변형의 찌그러짐을 확인할 수 있다.
[외적]
드디어 기다리고 기다리던 외적에 대해서 배울 수 있다.
위의 모든 것이 외적을 하기 위한 것이라 해도 과언이 아니다.
외적은 3차원 공간에서 정의할 수 있으며 다음과 같이 정의한다. (외적의 크기는 따로 유도해야 한다.)

행렬의 곱처럼 교환법칙이 성립하지 않음을 알 수 있다. (교환된 외적끼리는 서로 반대 방향을 갖는다.)
연습을 하기위해 다음 사실들을 직접 유도해보자.

외적의 결과는 내적의 결과와는 다르게 어떤 새로운 벡터로 나온다는 것을 알 수 있는데 때문에 방향이 중요한 요소로 작용한다. 외적을 계산하지 않고도 방향을 예측하려면 오른손 법칙을 쓰면 된다.
x를 시작하여 y를 감싸는 방향으로 손아귀를 말면 엄지의 방향이 외적의 방향이 된다. 물론, 두 벡터에 대해서 동시에 수직이다. (x, y와 외적의 내적이 0임을 직접 검증할 수 있다.)

외적을 정의했다면 3차원 공간의 세 번째 축을 정의할 수 있다.

일반적으로 z축은 위에 보이는 것처럼 나타낸다.
'학부 공부 - 수학 > 미적분학' 카테고리의 다른 글
| 다변수 미적분학:: 2. 점, 선, 면 (2) | 2023.12.21 |
|---|---|
| 다변수 미적분학:: 0. 개요 (0) | 2023.12.20 |