일반물리I:: 6. 충돌
질량 중심(Center of Mass)
한 점에 물체의 모든 질량이 모여있는 것처럼 거동하는 점을 질량중심이라고 한다.

질량줌심을 기준으로 이동을 생각하면 운동을 단순화할 수 있다.

위의 식이 이산적인 계(입자 n개)에서의 질량중심이고
아래의 식이 연속체의 질량중심이다.
물론 x만 나타냈지만 말이다.

이산합은 위와 같이 표현할 수 있다.
항을 두 개로 줄여본다면 어디서 많이 본 식이 나온다.


내분점 공식과 비슷한 모양이다.
머릿속으로 그림을 그려보면 더 질량이 큰 입자 쪽으로 질량줌심이 쏠리는 것은 당연하다.
비슷하게 수학에서 배운 무게중심 공식을 떠올려보자.
입자에 할당되는 질량이 모두 같다고 가정하면

이 역시 같은 식으로 나온다!
연속체에 관한식은 삼중적분으로 되어있는데 벡터 미적분학 카테고리에서 다룰 것이다.
현실에서나 삼중적분을 쓸 것이고 개념을 배울 때는 일차남짓 이차원까지만 다루므로 적분, 이중적분에 대한 식을 쓴다.
δ는 밀도에 관한 함수식이고 3차원에서는 부피밀도, 2차원은 면밀도, 1차원에서는 선밀도라고 부른다. (이렇게 부르는 것은 이후에도 계속 나온다.)
일반적으로는 밀도가 균일한 물체를 다루므로 δ는 상수로써 빠져나올 수 있다.
이때 최종적으로 다음식이 된다.

우변은 도심(형상의 중심, centroid)의 계산식과 똑같다.
단면 1차 모멘트라고도 한다.
유체역학을 비롯한 다양한 곳에 나오지만 한번 언급해봤다.

중적분을 배워야하겠지만 우리는 위와 같은 모양의 COM도 계산할 수 있다.

꽉 찬 원의 COM을 x_com이라고 하고 초승달 모양의 COM을 x'_com이라고 하면 위와 같이 유도할 수 있다.

작은 두 모양의 COM끼리의 COM이 원의 COM이다.
물체에 뉴턴 법칙을 적용하면 질량 중심에 법칙을 적용하는 것과 모양이 같다.
우리가 아는 F=ma의 식을 다음과 같이 표현할 수 있다.

운동량&충격량

운동량(Momentum)은 물체의 질량과 속도를 곱한 벡터량이다.
뉴턴 법칙이 여기서 시작했다고 해도 과언이 아니다.
운동량을 미분하면 힘이 나온다.

운동량의 변화량을 측정하면 힘이 어떻게 가해지는지 알 수 있다.
여러 입자로 구성된 물체의 운동량은 COM의 속도에 대한 식으로 나온다.
충격량(Impulse)은 다음과 같이 정의된다.

평균힘이 도출되는건 고등학교 때 물리를 하면서 봤겠지만 더 자세히 알고 싶다면 적분 평균값 정리를 보도록 하자.
https://ko.wikipedia.org/wiki/%ED%8F%89%EA%B7%A0%EA%B0%92_%EC%A0%95%EB%A6%AC
평균값 정리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. (a, f(a))와 (b, f(b))의 연결선을 아래로 평행 이동하여 어떤 점 c에서의 접선을 얻을 수 있다. 미적분학에서 평균값 정리(平均-定理, 영어: mean value theorem, MVT)는 대
ko.wikipedia.org
나중에 미적분학의 다양한 정리들을 증명하는데 쓰이니 알아두면 좋다.
운동량 보존 법칙
고등학교때 배운거랑 같다.
운동량은 벡터이기 때문에 각 성분들끼리도 보존법칙이 성립한다.

Pass
다양한 충돌
탄성 충돌
운동에너지가 보존되는 충돌이다.
에너지 보존법칙에 의해 다음이 성립한다.
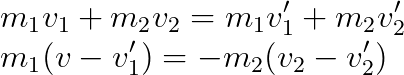
운동에너지도 보존되므로



(1)식에서 질량과 속도의 아랫첨자가 같은 부분을 운동량 보존식을 써서 모두 치환하였다.
이후 계산은 간단하다.
같은 방법으로 (2)식도 계산하면 최종적으로는 다음 식이 탄생한다.

비탄성 충돌
현실세계의 거의 대부분의 경우에는 비탄성 충돌이 일어난다.
비탄성 충돌에는 에너지가 열에너지로 소실되어 운동에너지 보존법칙은 일어나지 않는다.