고체역학:: 1. Tension, Compression, Shear
개요
기계공학에서 배우는 4대 역학은 동역학, 열역학, 고체역학, 유체역학이다.
우린 그중에서 정역학의 일종이라고 할 수 있는 고체역학에 대해 공부할 것이다.
정역학은 단어 뜻 그대로 멈춰있는 상황을 역학적으로 분석한다.
이는 일반물리에서 배운 물체의 평형과 같은 상황에서 적용된다.
알짜힘이 0이며(이동하지 않으며) 토크(회전하지 않는다)가 0인 조건에서 물체 내부의 변형, 이를테면 전단, 비틀림 등을 적용한 상태에서 물체를 분석하는 것이 고체역학이라고 할 수 있다.

Normal Stress&Strain
기본 가정이 들어가야 한다.
먼저 늘이고 줄이는 물체는 Prismatic bar, 기둥 모양이며 힘은 기둥의 중심축을 따라 가해진다.
그리고 물체는 균일하다.

Normal stress는 압력과 단위가 같다. 일반물리에서 p를 압력이라고 치고 공부한 적이 있었다면 의아할 수도 있겠지만 이 부분에서는 P라는 힘이 물체 양옆에 가해졌다고 가정한다. (면 벡터에 평행이라 Perpendicular의 약자를 딴 것이기도 하다.)
Strain은 우리말로 변형율 정도로 말할 수 있는데, 초기 길이 L에 대해 변화된 길이 δ의 비율로 계산된다.
어떤 봉을 P의 힘으로 잡아당긴다고 하자.
이때 한쪽이 고정되어 있는 경우와 양쪽을 P로 잡아당기고 있는 경우는 힘이 P만큼 가해진다고 말할 수 있다.
양쪽에서 잡아당기는 상황에서는 2P의 힘을 가하는 것이 아니다.
Stress-Strain Diagram
물리와 화학을 공부해 보면 실험적으로 검증된 개념이 매우 많다는 것을 알 수 있다.
본 그래프도 여러 물체를 수도 없이 늘려보면서 실험적으로 보인 경향성을 나타낸 것이다.
모든 물체가 이 그래프를 따르는 것은 아니지만 보통은 이 그래프를 따른다고 보면 된다.

각 축을 stress와 strain으로 잡아서 그린 그래프이다.
가로축은 총 네 부분으로 나눌 수 있고 각각 Linear region, Perfect plasticity, Strain hardening, Necking 단계이다.
Linear region에서는 고무줄을 늘였을 때 다시 돌아오는 것처럼 원래 상태로 돌아오는 과정을 거친다.
이때 물체는 Elasticity를 띄며 그래프를 거의 따라서 길이가 변하게 된다.

Linear region과 Yielding 사이 단계에서는 물체가 서서히 탄성력을 잃는다.
고무줄을 적당히 세게 잡아당겼다가 놓으면 처음보다 헐렁해지는 현상과 같다.

변형되어 길이가 달라진다.
이를 Partially elastic이라고 한다.
Yielding 단계는 엿가락을 늘이는 모습을 상상하면 된다.
엿가락을 늘이면 당연히 돌아오지 않는다.
이때부터 물체는 Plasticity를 띤다.
Stain hardening에서는 이상하게도 물체에 가하는 힘이 갑자기 증가하는 현상이 발생한다.
힘을 계속 가하다가 Ultimate stress를 찍으면 Necking이 일어난다.
유튜브에서 아무 생각 없이 보기 좋은 영상 중에 철근이나 플라스틱을 늘리는 영상들이 있는데 여기서 Necking을 볼 수 있다.
https://youtu.be/M7OyH0wNTrY?si=bz2WBRWxAYdAZbgK
영상처럼 철이 점점 늘어나다가 끊어지는데 이때를 Frature라고 한다.
훅의 법칙
고등학교 때도 배웠던 훅의 법칙이 여기서도 나온다.
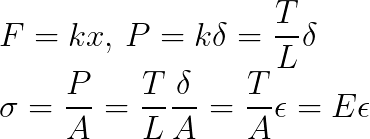
x와 δ는 의미적으로 같으니 동일하다.
용수철 상수 k는 어떤 길이를 늘일 때 필요한 힘(T/L)으로 바꿔서 표시했다.
마지막에 나오는 식 σ = E δ를 보면 F=kx와 매우 비슷하게 생겼다는 것을 알 수 있다.
E는 Modulus of elasticity 또는 Young's modulus라고 부른다.
Shear Stress&Strain
이전에 Normal stress부분과 매우 유사하다.

V가 물체에 가해지는 힘이다.
Normal stress와 다른 점은 면 벡터에 직교하는 힘이라는 것이다. (이도 역시 Vertical의 약자를 따서 V라고 표현한다.)

shear strain 또한 normal strain처럼 무차원 물리량이다.
외 힘이 4개나 가해지냐는 의문이 생길 수도 있다.
물체가 자유로이 움직일 수 있는 상태라면 면에 직교하는 힘이 가해질 때 힘에 이끌려서 이동하고 회전한다.
이러한 경우를 분석하는 것은 의미가 없다.
물체의 변형에 관해서 공부하는 것이므로 물체가 최소한의 범위 내에서 정지해 있는 상태를 다룬다.
따라서 개요에서 언급했던 것처럼 알짜힘과 알짜모멘트가 0인 상황을 가정한다.

물체 윗면에 힘을 가하면

힘의 평형이 유지되어야 하기 때문에 반대면에 같은 힘이 반대로 작용해야 하고

두 힘만 있으면 토크가 걸려 회전하기 때문에 모멘트의 평형을 맞추기 위해 옆면에도 힘이 작용한다.
훅의 법칙

G는 shear modulus of elasticity라고 한다.
Normal stress에 대한 훅의 법칙과 식이 매우 비슷하게 보이는데 둘을 통합할 수 있는 방법이 있을 것 같다.
+푸아송 비
고무줄을 늘이면 얇아지는 것처럼 물체가 변형되면 부피가 유지되어야 일반적이라고 할 수 있다.
이때 물체를 늘이는 방향의 길이 변화를 ε, 그에 직교인 방향의 길이 변화를 ε'라 두면 푸아송 비는 다음으로 정의된다.


일반적으로 푸아송 비는 0.3~0.4의 값을 갖는다.
푸아송 비를 이용하면 normal modulus와 shear modulus 사이의 관계를 나타낼 수 있다.

유도는 이후에 다룬다.
추가
고체가 변형된 것을 나타내는 그림들은 대부분 공부하는 입장에서 알아먹기 쉽도록 매우 과장해서 늘리거나 전단시킨 상태의 그림이다.
고무줄 같은 것을 제외하고는 철, 나무 등의 물체들은 실제로 매우 적게 길이가 변하거나 전단된다. (탄성을 띄는 범위에 한해서)